算子基本概念

算子名称（Name）

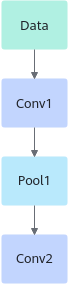
算子的名称，用于标志网络中的某个算子，同一网络中算子的名称需要保持唯一。如下图所示Conv1、Pool1、Conv2都是此网络中的算子名称，其中Conv1与Conv2算子的类型为Convolution，表示分别做一次卷积运算。

算子类型（Type）

网络中每一个算子根据算子类型进行算子实现的匹配，相同类型的算子的实现逻辑相同。在一个网络中同一类型的算子可能存在多个，例如上图中的Conv1算子与Conv2算子的类型都为Convolution。

张量（Tensor）

Tensor是算子计算数据的容器，TensorDesc（Tensor描述符）是对Tensor中数据的描述。TensorDesc数据结构包含如下属性如表1所示。

形状（Shape）

张量的形状，以(D0, D1, … ,Dn-1)的形式表示，D0到Dn是任意的正整数。

如形状(3,4)表示第一维有3个元素，第二维有4个元素，(3,4)表示一个3行4列的矩阵数组。

形状的第一个元素对应张量最外层中括号中的元素个数，形状的第二个元素对应张量中从左边开始数第二个中括号中的元素个数，依此类推。例如：

物理含义我们应该怎么理解呢？假设我们有这样一个shape=(4, 20, 20, 3)。

假设有一些照片，每个像素点都由红/绿/蓝3色组成，即shape里面3的含义，照片的宽和高都是20，也就是20*20=400个像素，总共有4张的照片，这就是shape=(4, 20, 20, 3)的物理含义。

如果体现在编程上，可以简单把shape理解为操作Tensor的各层循环，比如我们要对shape=(4, 20, 20, 3)的A tensor进行操作，循环语句如下：

produce A {
  for (i, 0, 4) {
    for (j, 0, 20) {
      for (p, 0, 20) {
        for (q, 0, 3) {
          A[((((((i*20) + j)*20) + p)*3) + q)] = a_tensor[((((((i*20) + j)*20) + p)*3) + q)]
        }
      }
    }
  }
}

轴（axis）

轴是相对shape来说的，轴代表张量的shape的下标，比如张量a是一个5行6列的二维数组，即shape是(5,6)，则axis=0表示是张量中的第一维，即行。axis=1表示是张量中的第二维，即列。

例如张量数据[[[1,2],[3,4]], [[5,6],[7,8]]]，Shape为(2,2,2)，则轴0代表第一个维度的数据即[[1,2],[3,4]]与[[5,6],[7,8]]这两个矩阵，轴1代表第二个维度的数据即[1,2]、[3,4]、[5,6]、[7,8]这四个数组，轴2代表第三个维度的数据即1，2，3，4，5，6，7，8这八个数。

轴axis可以为负数，此时表示是倒数第axis个维度。

N维Tensor的轴有：0 , 1, 2,……，N-1。