昇腾社区首页
中文
注册
开发者
下载
支持

MC²算子性能调优案例

案例介绍

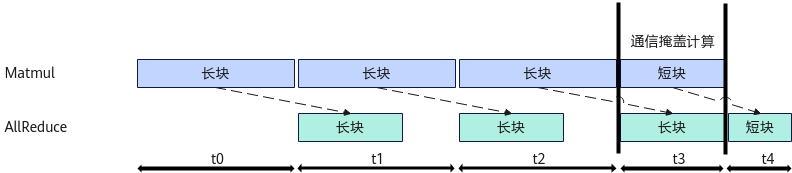
MC2通算融合算子的性能收益主要来自于通信、计算的并行执行，即将输入数据切分为多个子块，子块的计算和通信任务形成两条流水线，通过两条流水线上任务的并行执行，实现流水掩盖，从而提升算子性能。如下图所示，MC2算子先做Matmul计算、后通信的场景，输入矩阵沿M轴被切分为两块，第二块数据的Matmul计算和第一块数据的通信可以并行执行，从而达到计算和通信时间相互掩盖的目的。本节的所有图示中MM代表Matmul计算，hcom代表通信任务。

本案例将介绍如何分析通算融合算子的性能收益、如何制定较好的数据切分策略。更多MC2算子的完整样例请参考MatmulAllReduce样例、MatmulReduceScatter样例、AllGatherMatmul样例。

获取性能数据

通过msProf算子调优工具获取算子性能数据：

  • 获取真实环境执行的性能数据，包含各个流水的占比情况；
  • 获取仿真性能数据（指令流水图），包含各个流水的占用区间，可观察流水间依赖情况，从而优化并行效率。

分析主要瓶颈点

MC2算子性能收益公式为：

融合前算子串行耗时 = 融合前计算算子耗时 + 融合前通信算子耗时

MC2算子收益 = (融合前算子串行耗时 - 融合后MC2算子耗时) / 融合前算子串行耗时

融合后MC2算子的执行耗时，受以下因素制约，从而影响算子性能收益。

  • 因素一：计算和通信的执行时间差异

    若计算和通信任务的执行时间相差不大，则融合后，MC2算子的计算和通信并行执行，能得到较好的流水掩盖，性能收益较大。

    若计算和通信任务的执行时间差异较大，则融合后，MC2算子内计算和通信并行执行，能够掩盖的时间较少，算子整体执行耗时与未切分串行时的算子执行耗时接近，此时无法获得较大性能收益。

  • 因素二：数据切分导致的计算或通信的执行时间膨胀

    当对输入数据进行切分后，原本的整块数据被切分成若干小数据块，对若干小数据块分别做Matmul计算或者执行通信任务，此时相比切分前，计算或者通信任务的执行时间可能发生膨胀（即执行时间变长）。该膨胀产生的原因包括：切分后的数据块过小导致计算或通信的效率降低、切分的数据块过多导致增加额外的调度开销、并行执行后计算和通信对L2 Cache或device存储内存的访问冲突等。以Matmul计算为例，简单说明数据切分后执行时间可能发生的膨胀情况。

    • 未发生膨胀：

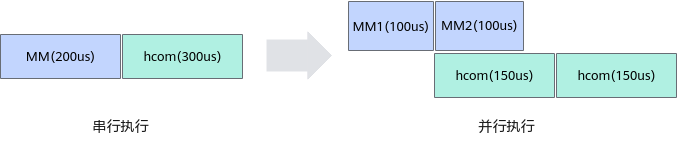
      数据切分前，Matmul执行时间为200us，将Matmul的输入均匀切分为两块，假设切分后，每块数据的Matmul执行时间都是100us，通过计算的并行执行，下图实际性能收益为100us。

    • 发生一般程度的膨胀：

      数据切分前，Matmul执行时间为200us，将Matmul的输入均匀切分为两块，假设切分后，每块数据的Matmul执行时间都是150us，通过计算的并行执行，下图实际性能收益为50us。

    • 发生严重程度的膨胀：

      数据切分前，Matmul执行时间为200us，将Matmul的输入均匀切分为两块，假设切分后，每块数据的Matmul执行时间都是200us，通过计算的并行执行，下图实际性能收益为劣化50us。

综合上述分析，计算和通信执行时间较均衡的场景，有更好的流水掩盖和性能收益；同时，性能收益也受到数据切分导致的执行时间膨胀的影响。下文将介绍如何制定数据切分策略，以达到最佳流水掩盖效果。

设计优化方案

以 Atlas A2 训练系列产品/Atlas 800I A2 推理产品/A200I A2 Box 异构组件 ，输入数据格式为ND、数据类型为half的MatmulAllreduce算子为例，该算子中计算执行在前，通信任务执行在后。假定Matmul计算中左矩阵的形状为[M, K]，右矩阵的形状为[K, N]，算子中的通信对象为Matmul的输出矩阵，则通信任务的输入shape为[M, N]。因为K轴只在Matmul计算中存在，当K轴较大时，计算量大，计算执行时间大于通信执行时间，此时计算为算子的瓶颈（bound）；反之，当K轴较小时，计算量小，计算执行时间小于通信执行时间，此时通信为算子的瓶颈。在制定数据切分策略前，对原始矩阵分别执行计算和通信任务，根据两个任务的执行时间判定bound场景。

该算子的数据切分策略应满足如下要求：

  • 只切分M轴。因为通信任务调用的Hccl API要求分块数据内存连续，若按N轴切分，则每行数据都被切断，导致通信数据的内存不连续，不满足通信要求；若按M轴切分，则每行数据都是内存连续的，满足通信要求。
  • 若A表示长块、B表示短块，只能切出A或B连续排布的形式，例如AAAB、BAAA等情况。

如上文所述，数据切分的目标是达成尽可能多的流水掩盖。根据计算与通信任务的执行时间差异，实际场景可以分解为如下两个具体场景，两个场景有各自细分的切分目标。

  • 计算bound：

    对于同一个切分后的数据块，计算执行耗时大于通信执行耗时，此时，计算连续，且通信的尾块要短，如下图所示。

    图1 计算bound示意图
  • 通信bound：

    对于同一个切分后的数据块，通信执行耗时大于计算执行耗时，此时，通信连续，且计算的头块要短，如下图所示。

    图2 通信bound示意图

前置工作：

在进行最终的数据切分前，需要做的前置工作有：判定bound场景、分别对Matmul计算和AllReduce通信的数据量与执行时间关系做公式拟合。具体步骤如下。

  1. 将输入数据分别单独执行Matmul计算和AllReduce通信任务，利用msProf工具分别采集执行时间，判定时间较长的任务为对应的bound场景。例如通信执行时间大于计算执行时间，则为通信bound场景。
  2. 将输入数据按M轴切分，分别切成M轴为256、512、768、1024、2048的若干数据块，这里可以根据实际情况调整切块大小。
  3. 将步骤2得到的数据块分别做AllReduce通信，利用msProf工具采集执行时间，得到每个数据块的执行时间t1, t2, ..., tn。然后，作图分析数据量与对应的执行时间的关系，拟合得到公式t = CostComm(m)，其中m表示数据块的M轴长度，t表示数据块的通信执行时间，CostComm表示拟合得到的m和t的映射关系。该映射关系一般为线性，若不满足线性关系，可以采用分段拟合的方式。示例如下：

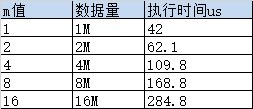
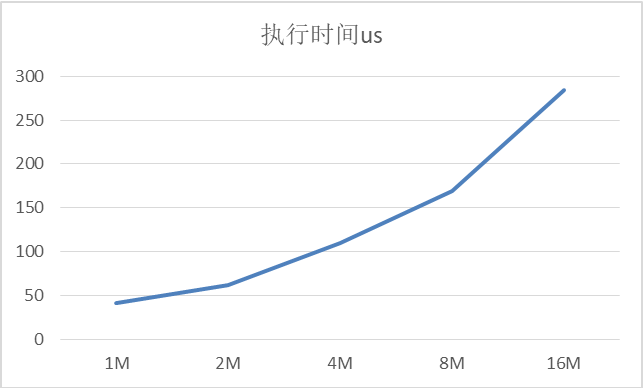
    数据量x = m * N * sizeof(dataType)，单位是Bytes。该拟合公式表示为：

    • x小于8MB：t = -0.9698202 * x * x + 27.0622573 * x + 14.769，单位是us。
    • x大于等于8MB：t = 13.58491263 * x + 61.508333，单位是us。
  4. 将步骤2切分得到的各数据块做Matmul计算，按与步骤3相同的方式采集各数据块的计算执行时间t，并拟合得到M轴长度和计算执行时间关系的公式t = CostMM(m)，CostMM示拟合得到的m和t的映射关系。

切分算法步骤：

  1. 根据输入矩阵的shape：M、K、N，按照经验值设置合适的M轴方向切分的短块长度。如下表达式中，a、b、c表示根据经验值给出的短块长度的备选，将K、N带入如下三个表达式后，取a、b、c的最小值m0为选定的短块长度。
    • a * K * N >= 4 * 1024 * 1024 * 1024，a取不等式的最小值
    • b * K * N / 1024 + b * N >= 6 * 1024 * 1024，b取不等式的最小值
    • c >= 3 * 128，c取不等式的最小值
    • m0 = min(a, b, c)
  2. 根据短块长度m0和拟合公式，分别得到计算执行时间t0 = CostMM(m0) * 1.15，通信执行时间t1 = CostComm(m0) * 1.15。

    注意：通信和计算并行执行时，可能出现抢占内存带宽的情况，导致执行时间增加，一般按经验在拟合公式中乘以1.15的系数，用户可以根据实测情况调整该系数。

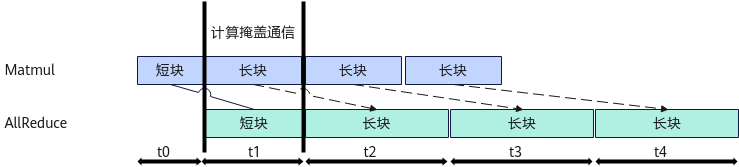
  3. 根据短块的长度，按图1或图2配平通算，得到长块的长度，长块长度尽量对齐128个元素，以保证计算亲和。本案例为通信bound场景，这里的配平，即将短块的通信时间和长块的计算时间匹配相等：将t1作为长块的计算执行时间，带入t1 = CostMM(m1)公式，计算得到m1，即为长块的长度。
  4. 根据短块长度m0、长块长度m1、原始M轴长度M，得出长块的切块个数count = (M - m0) / m1。该式一般不能整除，此时需要做如下处理：
    • 将结果的小数部分舍弃，保留整数部分作为切块个数。
    • 由于舍弃了小数部分，M轴长度有剩余，因此需要调整长块长度m1 = (M - m0) / count。
    • 为保持计算亲和，将长块长度m1调整至128对齐，即向下取128倍数的整数，更新长块长度m1。
    • 由于调整m1后，M轴长度有剩余，因此调整短块长度m0 = M - (m1 * count)。
    • 最终得到短块长度m0，长块长度m1，长块个数count。

验证优化方案性能收益

  • 制定切分策略并验证性能收益

    本MatmulAllreduce案例中，给定的输入矩阵Shape为M=4096，K=3072，N=8192，数据类型为half，分核数为8，通过融合前msProf工具采集，得到该输入的Matmul计算执行时间为803us，AllReduce通信的执行时间为1071us，总耗时1874us，属于通信bound场景。按照上述的切分算法，本案例的具体切分情况如下：

    1. 根据经验值选定短块（bound场景中短块为头块，即切分后的第一个数据块）M方向长度m0为384，则通信数据量x为：384 * 8192 * 2 / 1024 / 1024 = 6MB。按通信拟合公式估算通信的执行时间为143us。考虑可能会发生内存带宽冲突，因此再乘以1.15的系数，得出通信执行时间164us。
    2. 计算长块M方向长度。根据短块通信时间，配平长块的计算执行时间同样为164us，按计算拟合公式估算出该长度m1为768。
    3. 根据M=4096、m0=384、m1=768，计算长块个数：(4096 - 384) / 768 = 4.83，向下取整为4。
    4. 根据短块长度m0=384，长块个数4，调整长块m1长度：(4096 - 384) / 4 = 928，向下按128对齐，调整m1为896。
    5. 根据长块长度m1=896，长块个数4，调整短块m0长度：4096 - 896 * 4 = 512。
    6. 最终得到将原始输入矩阵切分为5个数据块，长度分别为：{512，896，896，896，896}。
    如下代码所示，在算子的Tiling代码中设置制定好的切分策略。按该切分策略测试，融合后该算子的执行时间为1262us，则融合算子的性能收益为(1874 - 1262) / 1874 = 32.7%。 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
    		 
    MatmulAllReduceCustomTilingData *tiling = context->GetTilingData<MatmulAllReduceCustomTilingData>();
tiling->param.rankDim = 8;
tiling->param.tileM = 512; // 短块大小
tiling->param.tileNum = 1; // 短块个数
tiling->param.tailM = 896; // 长块大小
tiling->param.tailNum = 4; // 长块个数
tiling->param.rankM = 4096;
tiling->param.rankN = 8192;
tiling->param.rankK = 4096;
tiling->param.isTransposeA = 0;
tiling->param.isTransposeB = 0;
tiling->param.cToFloatLen = 0;
tiling->param.nd2NzWorkLen = true;
tiling->param.dataType = static_cast<uint8_t>(HCCL_DATA_TYPE_MAP.at(aType));
  • 针对切分膨胀做调整

    上文提到，切分数据会引起计算或通信执行时间的膨胀，使实测结果与理论值有偏差。比如切块数量较多时，执行时间的膨胀对性能影响较大，可能导致性能收益变小或者出现性能劣化，因此最终需要根据上述理论切分策略，结合实测，对切分策略做调整。

总结

MC2算子通过数据切分后计算和通信的并行执行，获得性能收益，但受数据切分后执行时间膨胀的影响。对MC2算子进行性能调优的主要方式是制定数据切分策略，开发人员需要根据理论推导找到理想切分策略，然后根据实测结果调整，最终找到最优切分策略。

父主题： 优秀实践