Matmul算子性能调优案例
案例介绍
本案例对Matmul算子进行性能分析和优化。Matmul算子实现的功能是矩阵乘法,其中主要包含的流水为数据搬入和搬出流水,Cube计算流水。
以矩阵维度M = 4096,N = 5120,K = 4096,输入数据类型half,输出数据类型float,输出格式是ND为例,性能验证平台为Atlas A2训练系列产品/Atlas 800I A2推理产品,介绍针对Matmul算子的优化手段,包括优化分核逻辑、优化基本块、开启大包搬运。
- 分核逻辑:开启尽量多的Cube核使能并行计算。
- 优化基本块,选择最优的baseM、baseN、baseK参数,其中baseM、baseN、baseK为Matmul Tiling中的参数。
- 开启大包搬运:从GM搬运数据到L1时,对于A矩阵,一次搬入depthA1个基本块,基本块大小为baseM * baseK,对于B矩阵,一次搬入depthB1个基本块,基本块大小为baseN * baseK。使能大包搬运后,一次搬入的数据量变大,提升MTE2搬运效率。
获取性能数据
使用msProf工具获取算子的Profiling数据,重点分析MTE2,Cube,Scalar pipeline的流水情况。
分析主要瓶颈点
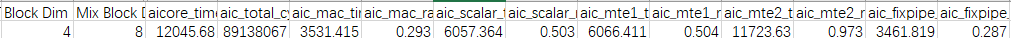
由以上Profiling数据,可以看出MTE2耗时占比较大,当前性能瓶颈点在于MTE2流水。
- Profiling数据的Block Dim可见分核未分满,考虑分核逻辑的优化。设CurrentCore是未优化前分核的Cube核数,MaxCore为最大Cube核数,当开启全部核并行做当前shape数据量的计算时,预估性能收益为MaxCore / CurrentCore的倍数。
- 优化基本块切分,将影响搬运数据的效率,算子搬运的总数据量为搬运的左矩阵和右矩阵数据量之和。根据矩阵乘法的算法,搬运左矩阵的次数为N / baseN,搬运右矩阵的次数为M / baseM,即搬运总数据量totalCnt = (N / baseN) * M * K + (M / baseM) * K * N。预估性能收益为搬运数据量的比值,优化前搬运数据量totalCnt0/优化后搬运数据量totalCnt1,化简后结果为(1 / baseM0 + 1 / baseN0) / (1 / baseM1 + 1 / baseN1),其中,baseM0, baseN0为优化前基本块参数,baseM1, baseN1为优化后基本块参数。
- 开启大包搬运后,指令条数变化、地址对齐等因素会影响性能,按照经验预估,对于MTE2为性能瓶颈的场景,会有20%+的MTE2性能收益。
设计优化方案
- 优化点一:优化分核逻辑
由Profiling数据看出分核数为4,启动更多的核同时计算,可以提高计算并行度。当前案例使用的AI处理器共20个核,每个核中包含1个Cube Core和2个Vector Core。NPU调用程序中设置blockDim为实际使用的核数20。
// 代码片段 uint32_t blockDim = 20; // 优化前blockDim为4 CHECK_ACL(aclInit(nullptr)); aclrtContext context; int32_t deviceId = 0; CHECK_ACL(aclrtSetDevice(deviceId)); CHECK_ACL(aclrtCreateContext(&context, deviceId)); aclrtStream stream = nullptr; CHECK_ACL(aclrtCreateStream(&stream)); uint8_t *aHost; uint8_t *aDevice; CHECK_ACL(aclrtMallocHost((void **)(&aHost), aFileSize)); CHECK_ACL( aclrtMalloc((void **)&aDevice, aFileSize, ACL_MEM_MALLOC_HUGE_FIRST)); ReadFile("./input/x1_gm.bin", aFileSize, aHost, aFileSize); // PrintData(aHost, 16, printDataType::HALF); CHECK_ACL(aclrtMemcpy(aDevice, aFileSize, aHost, aFileSize, ACL_MEMCPY_HOST_TO_DEVICE)); uint8_t *bHost; uint8_t *bDevice; CHECK_ACL(aclrtMallocHost((void **)(&bHost), bFileSize)); CHECK_ACL( aclrtMalloc((void **)&bDevice, bFileSize, ACL_MEM_MALLOC_HUGE_FIRST)); ReadFile("./input/x2_gm.bin", bFileSize, bHost, bFileSize); // PrintData(bHost, 16, printDataType::HALF); CHECK_ACL(aclrtMemcpy(bDevice, bFileSize, bHost, bFileSize, ACL_MEMCPY_HOST_TO_DEVICE)); uint8_t *workspaceHost; uint8_t *workspaceDevice; CHECK_ACL(aclrtMallocHost((void **)(&workspaceHost), workspaceSize)); CHECK_ACL(aclrtMalloc((void **)&workspaceDevice, workspaceSize, ACL_MEM_MALLOC_HUGE_FIRST)); uint8_t *tilingHost; uint8_t *tilingDevice; CHECK_ACL(aclrtMallocHost((void **)(&tilingHost), tilingFileSize)); CHECK_ACL(aclrtMalloc((void **)&tilingDevice, tilingFileSize, ACL_MEM_MALLOC_HUGE_FIRST)); CHECK_ACL(aclrtMemcpy(tilingHost, tilingFileSize, GenerateTiling(), tilingFileSize, ACL_MEMCPY_HOST_TO_HOST)); // PrintData(tilingHost, 16, printDataType::UINT32_T); CHECK_ACL(aclrtMemcpy(tilingDevice, tilingFileSize, tilingHost, tilingFileSize, ACL_MEMCPY_HOST_TO_DEVICE)); uint8_t *cHost; uint8_t *cDevice; CHECK_ACL(aclrtMallocHost((void **)(&cHost), cFileSize)); CHECK_ACL( aclrtMalloc((void **)&cDevice, cFileSize, ACL_MEM_MALLOC_HUGE_FIRST)); // ACLRT_LAUNCH_KERNEL(matmul_custom) // (blockDim, stream, aDevice, bDevice, cDevice, workspaceDevice, tilingDevice); matmul_custom_do(blockDim, stream, aDevice, bDevice, cDevice, workspaceDevice, tilingDevice);由于Matmul API都是从Vector侧发起的,当前案例使用的AI处理器中Cube Core和Vector Core的配比为1:2,所以在Matmul tiling计算中需要按照2倍的blockDim数切分,即Vector Core数。Tiling代码中,设置Tiling API按照40个核进行数据切分,如下代码所示。
int usedCoreNum = 40; // 优化前usedCoreNum是8 int runMode = 1; int32_t baseM = 64; // 64 int32_t baseN = 64; // 64 optiling::TCubeTiling tilingData; MultiCoreMatmulTiling tilingApi; tilingApi.SetDim(usedCoreNum);
图2 优化分核逻辑后Profiling数据
修改代码后,算子执行时间从12045us下降到2532us,约等于(20核 / 4核) = 5倍的性能提升。
- 优化点二:优化基本块
当前Tiling中设置的base块为 [baseM, baseN, baseK] = [64, 64, 256],这种基本块Cube计算cycle少,计算访存比(即计算量与需要数据量的比值)低;搬出一次Matmul结果到GM的base块是64 * 64,由于输出格式是ND,数据类型是float,搬出下一次Matmul结果的起始地址需要偏移一个baseN的大小,即64 * 4 = 256字节,导致fixpipe搬出时GM地址非512byte对齐,那么需要设置更优的基本块。
针对当前shape较大的场景,基本块的选择原则为计算访存比最大,即在Cube计算量最大的情况下,访存的数据量最小。在输入为fp16类型的情况下,Cube执行单元1 cycle能算16 * 16 * 16个数。根据经验,[baseM, baseN, baseK] = [128, 256, 64]和[128, 128, 128]两种切分方案均满足搬出时GM地址512Byte对齐(每搬出一次Matmul结果时,地址分别偏移256 * 4byte和128 * 4byte),Cube计算cycle数一致,为(128 * 64 * 256) / (16 * 16 * 16) = (128 * 128 * 128) / (16 * 16 * 16) = 512cycle。针对[baseM, baseN, baseK] = [128, 256, 64],计算访存比为512cycle / (128 * 64 * 2 + 256 * 64 * 2) = 512cycle / 48KB;针对[baseM, baseN, baseK] = [128, 128, 128],计算访存比为512cycle / (128 * 128 * 2 + 128 * 128 * 2) = 512cycle / 64KB;可见[128, 256, 64]基本块方案的计算访存比更高,计算密度更大,同样的计算量,需要的数据量最小,最大限度的提高Cube单元的计算量。
修改Tiling代码,通过SetFixSplit()接口设置baseM和baseN,tiling函数会自动计算出最优baseK,这里得到64。
int32_t baseM = 128; // 优化前baseM是64 int32_t baseN = 256; // 优化前baseN是64 optiling::TCubeTiling tilingData; MultiCoreMatmulTiling tilingApi; tilingApi.SetDim(usedCoreNum); tilingApi.SetAType(leftPos, leftFormat, leftDtype, bool(transposeA)); tilingApi.SetBType(rightPos, rightFormat, rightDtype, bool(transposeB)); tilingApi.SetCType(resPos, resFormat, resDtype); tilingApi.SetBiasType(biasPos, biasFormat, biasDtype); tilingApi.SetOrgShape(M, N, K); tilingApi.SetShape(M, N, K); tilingApi.SetFixSplit(baseM, baseN, -1);
使能这组基本块后,MTE2耗时(对应aic_mte2_time)从2452us降低到808us,MTE2性能提升3倍。
图3 优化基本块后Profiling数据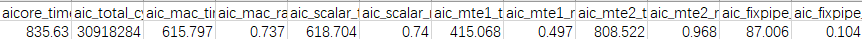
- 优化点三:使能大包搬运
当前带宽利用率为:totalSize / mte2Time = totalCnt * dtype / mte2Time,代入数据计算为2491GB/s。未使能大包搬运的情况下,矩阵从GM搬运到L1一次只搬运1个基本块。通过模板参数使能大包搬运,一次搬运多个基本块,提高MTE2带宽利用率。
// 原始matmul对象定义: Matmul<MatmulType<TPosition::GM, CubeFormat::ND, A_T>, MatmulType<TPosition::GM, CubeFormat::ND, B_T>, MatmulType<TPosition::GM, CubeFormat::ND, C_T>, MatmulType<TPosition::GM, CubeFormat::ND, BiasT>>> mm; // 通过在定义matmul对象的模板参数里加上CFG_MDL参数使能大包搬运功能: Matmul<MatmulType<TPosition::GM, CubeFormat::ND, A_T>, MatmulType<TPosition::GM, CubeFormat::ND, B_T>, MatmulType<TPosition::GM, CubeFormat::ND, C_T>, MatmulType<TPosition::GM, CubeFormat::ND, BiasT>, CFG_MDL>> mm;从下图可以看到,使能大包搬运后,MTE2耗时从808us下降到591us,带宽利用率代入数据计算为3406GB/s,利用率提升36%+,Cube利用率达到80%+。
图4 使能大包搬运后Profiling数据
验证优化方案性能收益
- 优化分核逻辑,实际收益4.75倍,约等于(20核 / 4核) = 5倍收益,并且考虑到核的启动开销,可以认为收益一致。
- 优化基本块,实际收益约3倍,理论评估带入上述分析公式,收益为(1 / 64 + 1 / 64) / (1 / 128 + 1 / 256),约等于2.7倍,考虑到cache缓存的影响,认为收益一致。
- 大包搬运,大包搬运实际收益25%+,与经验值一致。
总结
优化点一和优化点二的适用场景,需要shape足够大,数据量足够多,才能分满核和使能最优的基本块。大shape场景下,MTE2 Bound算子可参考此案例的优化手段。