理论参数
理论性能为算子实际性能的理想目标。不同的硬件平台的硬件规格各异,理论性能可以帮助我们了解硬件的潜能,从而设定性能优化的目标。
- 搬运相关流水(MTE1/MTE2/MTE3等)的理论耗时 = 搬运数据量(单位:Byte) / 理论带宽。例如:某款AI处理器的GM峰值带宽约为1.8TB/s,想要进行一次float数据类型、4096 * 4096大小的矩阵搬运,搬运的理论耗时是sizeof(float) * 4096 * 4096 / 1.8 TB/s = 37.28 us(按照1 TB =1012 Byte来计算)。

- 搬运指令同时存在时,会存在共享带宽的情况,并不能每条都以接近理论带宽的速率搬运数据。比如,当MTE2/MTE3同时进行GM读写时,搬运流水线的耗时应该是(MTE2搬运量 + MTE3搬运量)/ GM带宽。
- 搬运不同大小的数据块时,对带宽的利用率(有效带宽/理论带宽)不一样。针对每次搬运数据量较小的情况,实测性能达不到理论带宽。
- 计算相关流水(Cube/Vector/Scalar等)的理论耗时 = 计算数据量(单位:Element) / 理论算力。例如:某款AI处理器对float数据类型的Vector理论峰值算力为11.06 TOPS,想要进行一次32K float类型的Element单指令计算,计算的理论耗时是32 K / 11.06 TOPS = 0.003 us (按照1 K =1000来计算)。
查找瓶颈
获取性能数据后,和理论数值差异较大的地方、耗时较长的流程被认为是“瓶颈点”。下文将介绍如何通过性能数据找到瓶颈点和对应的优化方向。
- 方法一:通过上板Profiling分析流水情况
查看上板Profiling解析后的op_summary_*.csv文件分析流水情况。注:“*”表示时间戳。
图1 op_summary_*.csv示例一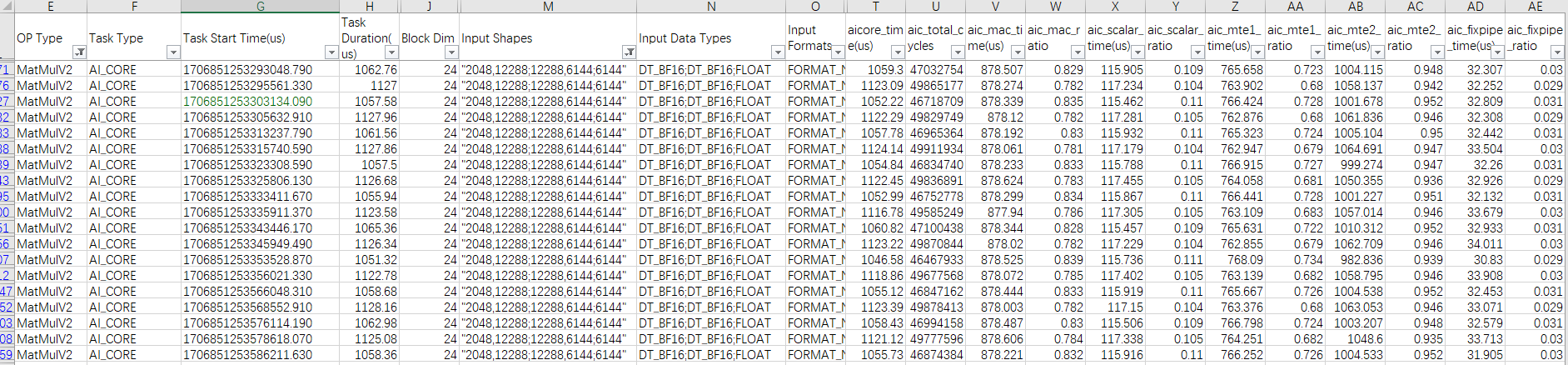
每条流水线的利用率理想情况下应为100%,没有达到100%的流水就可能有提升空间。上图示例中为某款AI处理器上获取的数据,可以看到Cube算子MatMulV2,Cube流水的利用率aic_mac_ratio在80%左右,初步判断没有充分发挥算力;MTE2流水的利用率aic_mte2_ratio已经在95%左右,判断MTE2是最长的流水。
然后比较最长的流水和理论的差距:输入左右矩阵的shape分别为(2048,12288)、(12288,6144),数据类型为bfloat16;Bias输入的shape为(6144),数据类型为float。由此可以计算出总共需要搬运的数据量,继而通过理论参数中介绍的搬运流水理论耗时计算方法计算出理论值为(sizeof(bfloat16) * (2048 * 12288 + 12288 * 6144) + sizeof(float) * 6144) / 1.8 TB/s ≈ 111.8 us (按照1 TB =1012 Byte来计算),与实际性能数据aic_mte2_time存在比较大的差距。经分析输入数据的总大小已经超过L1的空间(512KB),做MatMul计算会存在输入矩阵数据重复搬运的情况,重复搬运的次数是否合理,需要结合流水优化和Tiling优化手段进行优化,可参考方法三、查看仿真流水图分析各条流水的情况进一步分析。
图2 op_summary_*.csv示例二
上图示例中算子输入的shape为(8192,8192),数据类型为float。由此可以计算出总共需要搬运的数据量,继而通过理论参数中介绍的搬运流水理论耗时计算方法计算出理论值为sizeof(float) * (8192 * 8192) / 0.8 TB/s ≈ 335.5 us (按照1 TB =1012 Byte来计算,不同的AI处理器其理论带宽有差异),与实际性能数据aiv_mte2_time相符,可以判断该算子基本是一个搬运MTE2 bound(达到上限)的算子。本示例中总体执行时间Duration为350us,和MTE2的实际耗时持平,说明该算子已经调优完成。如果MTE2耗时和总体执行时间有较大差距,那么下一步优化方向主要是流水优化结合Tiling优化,使得其他的流水尽量隐藏在MTE2的流水中,可参考方法三、查看仿真流水图分析各条流水的情况进行进一步分析。
- 方法二:通过上板Profiling分析Tiling情况
查看上板Profiling解析后的op_summary_*.csv文件分析Tiling情况。
图3 op_summary_*.csv示例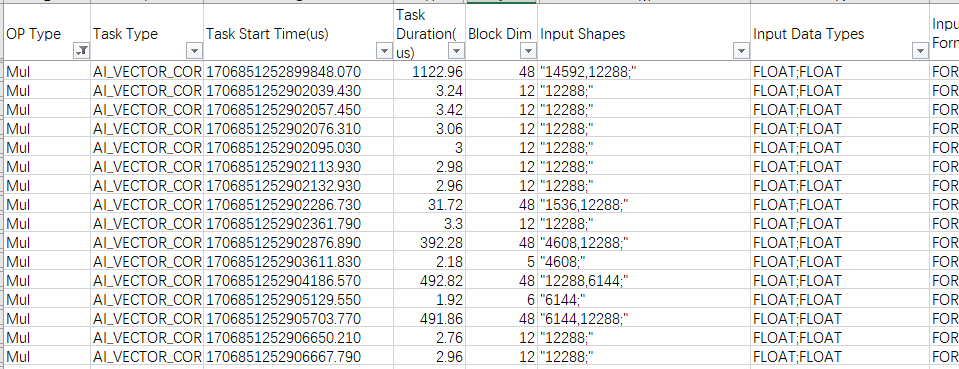
上图示例中为某款AI处理器上获取的数据,通过硬件平台可以查看该AI处理器有48个Vector核,Mul算子是一个纯Vector算子,但是有些场景没有用满所有Vector核(Block Dim < 48),造成算力浪费。那么下一步的主要优化方向为Tiling优化。
- 方法三:通过仿真流水图分析流水情况图4 仿真流水图示例
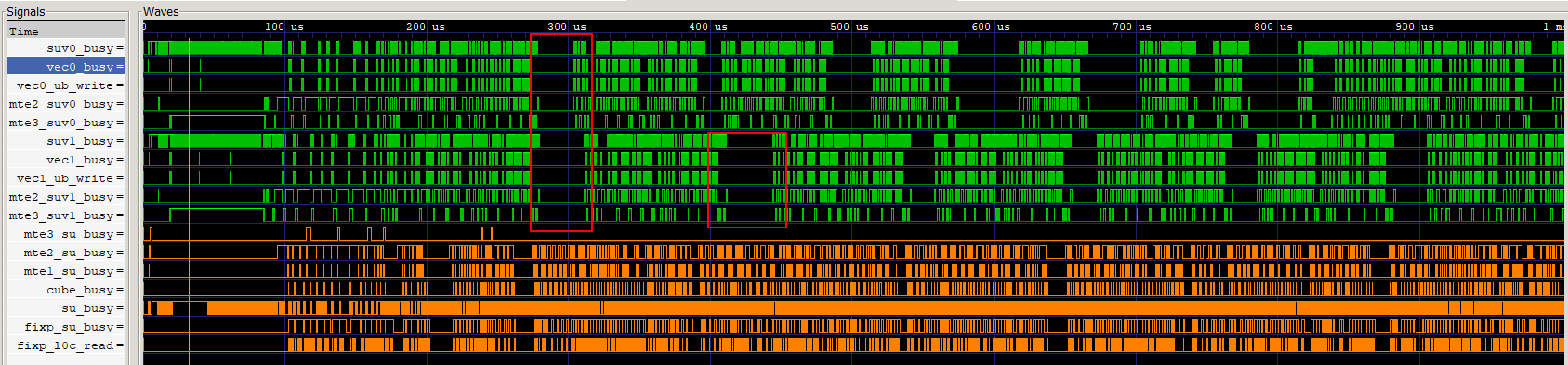
上图示例中为某款AI处理器上获取的数据,可以看到Vector核的相关流水(vec0的MTE2、MTE3,vec1的MTE2、MTE3等)有规律性的断流现象。可以结合算子逻辑分析,是否存在数据依赖等因素导致断流。那么下一步的主要优化方向为流水优化,其次结合Tiling优化和内存优化等手段进一步提升Vector流水利用率。
- 方法四:通过仿真流水图查看头开销(算子启动正式计算前的额外开销)图5 仿真流水图示例
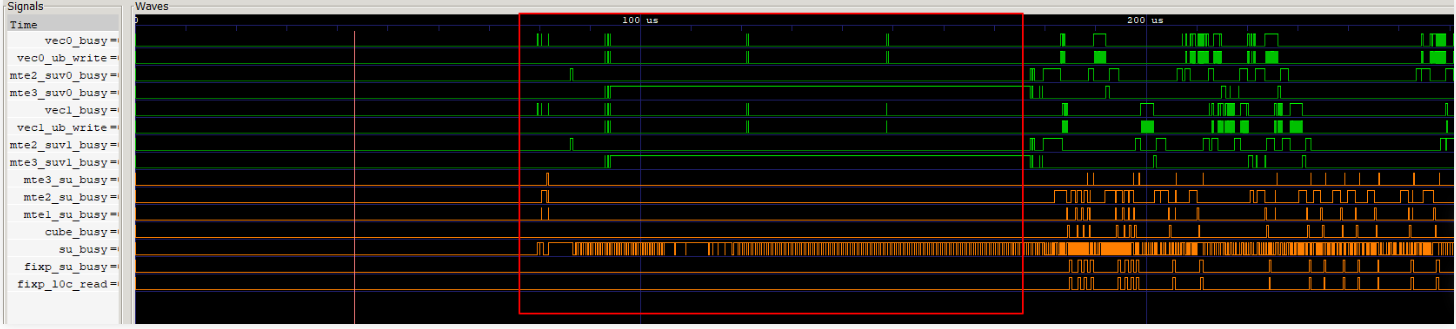
上图示例中为某款AI处理器上获取的数据,其中可以看到在算子启动正式计算前,被Scalar和MTE3两条流水占据,因而存在头开销。那么下一步的主要优化方向为搬运优化和指令优化,减少搬运时间和Scalar计算时间。