【昇腾热点算子大解密】CANN插值类算子启用矩阵化实现,性能提升10倍,助力多模态模型大幅增效
发表于 2025/08/12
插值技术:让数字世界“无缝衔接”的隐形推手
在深度学习的视觉世界中,插值操作如同空间魔术师,通过数学算法重新定义特征图的维度。当CT影像的断层切片需要拼接成完整3D模型,当自动驾驶摄像头的画面要转换为鸟瞰视角,当AI模型的高低层特征需要融合……这些“数据断层”的衔接,都依赖插值的精准计算。它像一位隐形的“数字裁缝”,通过已知信息推算缺失细节,让离散数据变得连续流畅。
作为PyTorch、TensorFlow等主流AI框架的核心操作之一,插值能够智能地缩放特征图尺寸,将低分辨率特征扩展为高清表达,或反向压缩高维特征以实现计算优化,支撑着现代AI视觉系统的核心场景。
在医学影像领域,3D U-Net(经典的医学影像分割模型)的上采样阶段,会用双线性插值将低分辨率特征图放大至原始病灶尺寸,确保肿瘤分割边界清晰;nnU-Net(医学影像通用框架)在预处理时,通过插值将不同设备的CT/MRI影像统一为标准尺寸,避免因设备差异导致的诊断偏差。
在自动驾驶场景中,BEVFormer(多模态3D检测模型)将摄像头的2D视图投影到鸟瞰图(BEV)时,用插值补全不同视角的重叠区域,让车辆精准感知周围障碍物;Faster R-CNN的特征金字塔(FPN)通过插值融合不同尺寸的特征图,让红绿灯、行人等小目标不被忽略。
计算机视觉领域更离不开插值。ResNet分类图像时,用双线性插值将特定大小的输入缩放至不同尺寸适配训练;YOLOv8的PAN结构用最近邻插值快速拼接不同尺寸的特征图,平衡检测速度与精度。
从医学影像的病灶重建到自动驾驶的实时感知,从AI模型的特征融合到日常的图片缩放,插值技术始终在填补数据缝隙。它不创造新信息,却让数字世界的每一次尺寸转换和模态衔接都自然流畅,成为智能技术落地的关键基建。
插值算子的功能概要
插值算子作为PyTorch(torch.nn.functional.interpolate)的核心空间变换操作,实现了多种维度的张量尺寸调整,通过数学算法对输入数据进行智能缩放:
- 上采样:扩展特征图尺寸(如32×32 → 256×256)
- 下采样:压缩特征图尺寸(如1024×1024 → 128×128)
- 非整数倍缩放:支持任意比例尺寸变换
支持的插值算法包括:
| 算法类型 | 适用维度 | 特点 | 典型场景 |
|---|---|---|---|
| 最近邻(nearest) | 1D/2D/3D | 速度快,边缘锐利 | 实时目标检测 |
| 线性(linear) | 1D | 平滑过渡 | 时序信号处理 |
| 双线性(bilinear) | 2D | 精度效率平衡 | 图像分类/分割 |
| 双三次(bicubic) | 2D | 高平滑度,质量最佳 | 超分辨率重建 |
| 三线性(trilinear) | 3D | 体积数据连续处理 | 医学影像重建 |
| ... | ... | ... | ... |
支持的数据格式包括:
| 格式 | 维度 | 结构说明 | 典型应用 |
|---|---|---|---|
| NCW | 1D | [批, 通道数, 宽] | 音频信号处理 |
| NCHW | 2D | [批, 通道数, 高, 宽] | 图像分类/目标检测 |
| NCDHW | 3D | [批, 通道数, 深, 高, 宽] | 视频分析/体数据重建 |
该函数已成为计算机视觉、医学成像、视频处理等领域的基础空间变换工具,在U-Net、YOLO等经典模型中承担特征图尺寸转换的关键职责。
插值算子的实现原理
PyTorch实现的插值算子实现采用空间位置并行化+通道向量化策略,将原始数据(NCW\NCHW\NCDHW)重组为向量计算单元,最大化利用现代硬件加速的并行计算能力。以下以双线性(bilinear)插值为例,说明实现原理。
在双线性插值中,对于给定的输出位置 (h_out, w_out),其对应的四个邻域点坐标和权重值在相同空间位置上对所有批次(N)和通道(C)都是相同的,这一特征带来了关键的可优化点。
# 伪代码,传统实现: 四重循环,逐点计算
for n in range(N): # 批次循环
for c in range(C): # 通道循环 ← 瓶颈!
for h_out in range(H_out):
for w_out in range(W_out):
# 计算权重和邻域坐标
w00, w01, w10, w11 = compute_weights(h_out, w_out)
# 获取四个邻域点值
v00 = input[n, c, y0, x0]
v01 = input[n, c, y0, x1]
v10 = input[n, c, y1, x0]
v11 = input[n, c, y1, x1]
# 加权求和
output[n, c, h_out, w_out] = w00*v00 + w01*v01 + w10*v10 + w11*v11
在传统方案中,对每个批次(N)和通道(C)进行循环,对H和W组成的矩阵中的点执行逐点计算。显然,这种方法需要对每个点都计算一次权重。结合前文中提到的,给定输出位置的相邻点的权重对所有批次和通道是相同的,基于此,我们提出的优化想法就是,将第一次计算得出的权重存储起来,在后续循环中通过查表获得权重,而非重新计算。这种优化方式能减少计算量,但仍然改变不了逐点计算的本质,循环控制以及频繁访存都会引入大量计算耗时。
我们进一步想到,将逐点的标量计算通过向量化计算重组,对于每个输出位置,一次性加载所有批次和通道的邻域数据,即形成长度为[N × C]向量,这样就可以利用NPU Vector指令级并行完成加权求和。这种优化方式可以带来缓存利用率的提升,将分散的通道访问转换为连续内存块加载,以提升缓存命中率。验证后发现,向量化计算可以消除传统实现中大量的循环开销(超90%),将计算效率提升至少4倍以上,特别在通道数大的场景(如ResNet的2048通道)效果更为显著。
# 伪代码,向量化实现:空间位置外循环,批次通道内聚
for h_out in range(H_out):
for w_out in range(W_out):
# 1. 计算权重和邻域坐标(所有NC共享)
w00, w01, w10, w11 = compute_weights(h_out, w_out)
y0, x0, y1, x1 = get_neighbor_indices(h_out, w_out)
# 2. 向量化加载所有通道和批次的邻域数据, [N, C] 维度被展平为向量
v00_vec = input[:, :, y0, x0] # 形状 [N × C]
v01_vec = input[:, :, y0, x1] # 形状 [N × C]
v10_vec = input[:, :, y1, x0] # 形状 [N × C]
v11_vec = input[:, :, y1, x1] # 形状 [N × C]
# 3. 向量化加权计算(单指令处理所有NC)
output_vec = (w00 * v00_vec + w01 * v01_vec + w10 * v10_vec + w11 * v11_vec)
# 4. 向量化存储结果
output[:, :, h_out, w_out] = output_vec
插值算法向量化计算后性能收益显著。当我们进一步分析性能流水时,发现其主要受限于以下瓶颈:
- 非连续内存访问瓶颈:当构建跨通道/批次的向量时(如input[:, :, y0, x0]),需要从全局内存中收集非连续存储的数据点,每个通道的数据间隔的字节数为H * W * sizeof(data type)。这种“跳跃式”访问模式导致访存带宽利用率急剧下降(40%~60%)。批次和通道数越大,访存影响越大;
- 缓存容量压力:多核并行处理时,每个核都需要加载自己分配到的数据,可能会造成高速缓存资源竞争,影响数据传输效率。
当前的硬件除了有高性能的Vector计算单元,还有Cube计算单元,其特点是用于矩阵乘加运算,算力巨大。至此,插值算法向量化计算算法仅使用了Vector计算单元,而Cube计算单元在计算过程中处于闲置状态。我们不禁想到,是否有可能将Cube计算单元也启用,充分释放硬件潜力,进一步提升插值算子性能?
插值算子的矩阵化实现,性能大幅提升
仍然以双线性(bilinear)插值为例,下图包含上采样和下采样的示意。

左图是上采样示意,右图是下采样示意。可以看到,上采样输出点(黄色点)周围有4个邻点;下采样输出点周围有更多的邻点,取决于下采样的缩小比例。无论是上采样或是下采样,其基本的计算逻辑一致,都是输出点的“邻点”集合的“加权求和”,只不过邻点的数量不同。将目标点与周围邻点的关系放在二维平面上,可表达为:
其中,y表示特定的输出点,xij表示与y相关的邻点,n表示邻点的数量。
以上采样为例,对周围的4个邻点的加权求和可以分解为两个步骤:先沿着横轴对2个邻居点(X00和X01、X10和X11)加权求和,得到Y1和Y2;再沿着纵轴对Y1和Y2加权求和,得到最终的输出Y点。
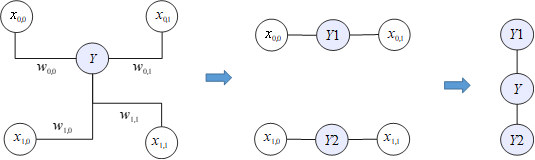
由此,双线性插值操作可以被分解为两个过程,先横向加权求和,再纵向加权求和。即,先执行一次横向插值,再执行一次纵向插值。加权求和这一步操作,符合矩阵乘的范式,因此,双线性插值可以写成:
由上述表达式可见,双线性插值可以通过两次矩阵乘完成。其中,X是原始数据,Wh和Wv分别是横向插值和纵向插值的权重矩阵,Y是插值后的输出数据。使用矩阵实现插值,优势在于:
- 可以充分使能高性能的Cube计算单元,昇腾NPU的Cube Core,其算力是Vector Core的10倍以上;
- 对于NCW、NCHW、NCDHW形式的输入数据,无需“跳跃式”访存,数据可以整段连续拷入芯片内的缓存单元,避免访存带宽利用率下降。

上图为使用矩阵乘算法实现双线性插值的实现示意。图中所示的是横向和纵向都是上采样的例子。假定原始数据(H, W) = (100, 120),横向放大2倍,纵向放大4倍,则右权重矩阵的shape = (120, 240),左权重矩阵的shape = (400, 100),对应输出数据(H_0, W_0) = (400, 240)。我们发现,直接将向量操作转化成矩阵乘的插值方案存在一个问题,即:权重矩阵过于稀疏。特别的,在上采样场景中,仅对角线附近为非0值,其余全是0(下采样场景由于输出点的邻点较多,权重矩阵也相对稠密的多)。如果不使用任何优化手段直接执行矩阵乘,显然会因为冗余的计算而浪费大量算力,最终性能可能反而不如经典的向量化算法。
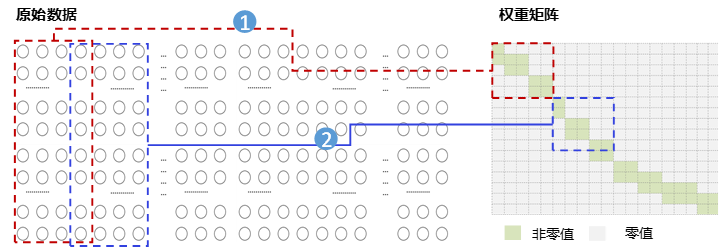
如上例,右权重矩阵的shape = (120, 240)过于稀疏。然而,插值操作的权重矩阵实际上是通过计算得到的,而非事先存在的原始输入。因此,我们想到可以每次构建权重矩阵的一小部分,避免堆积大量偏离对角线的0值,再从原始矩阵中截取对应的数据执行矩阵乘。这种方法可以显著减少权重矩阵的稀疏程度,极大缓解算力浪费问题。优化后,整个插值计算过程就涉及两步计算:权重矩阵构建,矩阵乘。
- 权重矩阵构建:首先需要计算权重,通过经典向量化方法算出权重向量,然后构造成矩阵格式。这部分需要用到Vector计算单元的算力;
- 矩阵乘:截取原始数据中相关的部分,然后与构造好的权重矩阵执行矩阵乘。
昇腾NPU的架构中,AICore包含了Vector Core和Cube Core,天然支持上述算法:Vector Core负责构造权重矩阵,Cube Core负责矩阵乘。两个独立计算单元可以很好地各司其职。
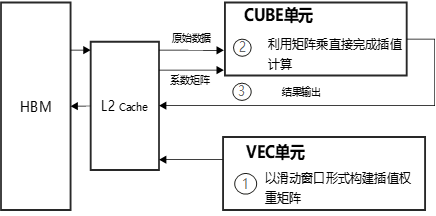
为了发挥NPU的算力优势,充分压榨硬件资源,就需要通过合理的流水排布策略,让Vector和Cube Core并行执行。插值算法的流水线设计,是让Vector Core持续不断地以滑窗的方式计算窗口区域内的权重矩阵;当权重矩阵构建完毕后,通过核间同步消息通知Cube Core执行矩阵乘。此时,Vector Core也不会闲置,将紧接着计算下一个窗口的权重矩阵,再发送同步消息,如此反复,直到插值操作完成。这种流水并行的计算方式,确保了Vector Core和Cube Core始终处于满载计算状态,有效避免了计算单元闲置,从而实现最优性能。
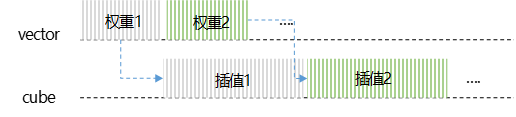
基于创新的矩阵化实现,未来也有很多探索的方向值得我们思考。比如,滑窗的窗口应该设置为多大合适?若窗口设置过小,虽然权重矩阵的稀疏程度更低,但截取原始数据式需要“跳过”更多的数据,造成带宽利用率降低;反之,窗口设置过大,截取原始数据式需要“跳过”的数据较少,带宽利用率高,但权重矩阵的稀疏程度会增大,造成算力浪费。类似的参数大小都是需要权衡的,依据原始数据的shape,放大\缩小的倍数等参数,选择合适的窗口大小,才能获得最大的性能收益。
结语
当前,CANN的插值算法优化已从传统的逐点计算演进至向量化并行,并进一步突破为矩阵化计算,通过Vector-Cube双核协同流水线,最大化释放NPU算力,这一创新实现了计算效率的阶跃式提升。随着AI向高维、实时、多模态方向发展,未来我们也会持续探索更多算法优化路径。
Upsample算子功能通过CANN软件包使能,社区版资源下载地址:
https://www.hiascend.com/developer/download/community/result?module=cann
算子接口定义为:
aclnnStatus aclnnUpsampleBilinear2dGetWorkspaceSize(const aclTensor *self, const aclIntArray *outputSize, const bool alignCorners,
const double scalesH, const double scalesW, aclTensor *out, uint64_t *workspaceSize, aclOpExecutor **executor)
aclnnStatus aclnnUpsampleBilinear2d(void *workspace, uint64_t workspaceSize, aclOpExecutor *executor, aclrtStream stream)
aclnnStatus aclnnUpsampleBicubic2dAAGetWorkspaceSize(const aclTensor* x, const aclIntArray* outputSize, const bool alignCorners,
const double scalesH, const double scalesW, aclTensor* out, uint64_t* workspaceSize, aclOpExecutor** executor)
aclnnStatus aclnnUpsampleBicubic2dAA(void *workspace, uint64_t workspaceSize, aclOpExecutor *executor, aclrtStream stream)详细接口文档可参考昇腾社区API描述:



